miscellaneous examples of non convex polyhedra

Reminder: A polyhedron is convex if all its diagonals are inside or on its surface.
A diagonal of a polyhedron is a segment joining two vertices and which is not an edge.

a few classical examples

compound of two regular triangular prisms
(prism with base a David's star)

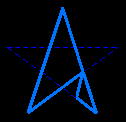
regular pentagrammic pyramid
(base: star pentagon)

regular pentagrammic prism
(uniform polyhedron)

a pentagonal star
(skeleton: golden triangles with same base)

pentagrammic bipyramid
(ten self intersecting equilateral triangles)

non crossed regular pentagrammic antiprism
(uniform polyhedron)

This uniform polyhedron, the tetrahemihexahedron, has only seven faces: four triangles and three squares going through the center and two by two orthogonal. Its twelve edges are the sides of the four triangles. It is a one-sided surface therefore non orientable.
This heptahedron is a faceted regular octahedron from which four regular tri-right-angled tetrahedra have been excavated.

The medial rhombic triacontahedron is the dual of the dodecadodecahedron (uniform polyhedron); it is a stellation of the rhombic triacontahedron with hidden interior pentagrammic vertices.

the small rhombihexahedron (uniform polyhedron)
(18 faces, among which 6 self-intersecting octagons)

and its dual: the small rhombihexacron
(24 "butterfly" faces: crossed symmetric quadrilaterals)

two curious equifacial dodecahedra

The faces of this dodecahedron are identical non convex symmetrical pentagons (piece of a pentagram). It has tetrahedral symmetry with only three reflection planes two by two orthogonal. Curiosity: by alternating this polyhedron with a regular dodecahedron you can fill the space.
The faces of this dodecahedron described by George Olshevsky are also identical non convex pentagons cut out from an acute golden triangle: a face is the assembling of two obtuse golden triangles (one vertex of the pentagon belongs to the opposite side). It has tetrahedral symmetry without reflection plan, thus exists in two mirror image versions.

an easy to build octahedron

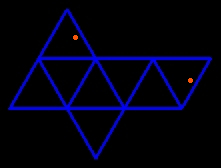
The net of this non convex deltahedron is also a net of the regular octahedron; this means that the two polyhedra have the same faces, but one is convex and the other isn't.

The two sides marked with a red point build the edge of the unique "valley fold".

two Möbius deltahedra (Roger Kaufman)

All the faces of these two polyhedra are equilateral triangles and all their edges belong to the symmetry planes.

tetrahedral symmetry (6 symmetry planes, 24 faces)

octahedral symmetry (9 symmetry planes, 48 faces)

two other nice deltahedra (Robert Dawson)

All the faces of these two polyhedra are equilateral triangles; "pockets" ("open" bipyramids) have been assembled to build closed rings.

7x(2x5) = 70 faces

3x(2x5) + 3x(2x4) = 54 faces

two non convex polyhedra with regular faces and intersecting pentagons (Richard Klitzing)

3 triangles, 3 squares and 3 pentagons

a toroid with 6 triangles and 6 pentagons

two compounds of three square prisms

On both compounds the intersection of the three prisms is a cube; hit "f" to see this hidden cube.

references:

• http://cs.stmarys.ca/~dawson/images3.html by Robert Dawson.
• Hedron by Jim McNeill

home page

convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects

January 2004
updated 08-08-2012