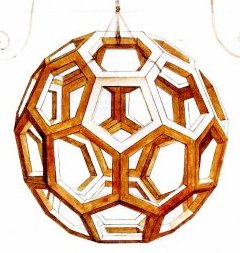
This truncated icosahedron represented with "solid edges" is one of the illustrations of The Divine Proportion (Lucas Pacioli)
The polyhedron on the top left of this portrait of Luca Pacioli is a glass small rhombicuboctahedron half-filled with water.


marble mosaic, Saint Mark's basilica in Venice
(small stellated dodecahedron)

polyhedra engraved on wood in the church of Santa Maria of Organo in Verona
|
|
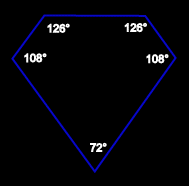
a pentagonal face |
| Its dual is a dodecahedron with triangular isosceles faces (triangular antiprism biaugmented by two tetrahedra). |
|

| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
• the four lines, the four columns and the two diagonals
• the four 2x2 squares of the corners and the one of the center
• the vertices of three "big" squares: 16+13+1+4 3+8+14+9 2+12+15+5
• the vertices of four rectangles: 3+2+14+15 5+9+12+8 3+5+14+12 2+8+15+9
The sums of two boxes symmetrical with respect to the center have all the same value 17=34/2
And on the bottom line there is also the date of completion of the engraving (1514).
There are two ways to build this polyhedron:
• excavate twelve triangular prisms on a cube truncated at the third by the vertices (in red),
• augment a cube truncated by the edges and the vertices (in green) with eight flat triangular antiprisms.

sculpture in a cemetery, Pays Basque (France)
(photo by André Brzezinski)
 |
 |
 |
 |
| dodecahedron Catania, Sicily |
small rhombicuboctahedron
castle of Flaugergues, Montpellier - monastery of Mount Sainte-Odile, Alsace - botanical garden of Strasbourg, Alsace |
||

Reptiles

Gravity

Stars
|
compound of two tetrahedra |
compound of two cubes |
small stellated dodecahedron |
|
stellated cuboctahedron |
compound of three octahedra |
|
compound of three cubes |
stellated rhombidodecahedron |
Waterfall



Sacrament of the Last Supper.
(the "cross" is a net of the hypercube)



