S'il semble naturel qu'une troncature du dodécaèdre régulier conduise à un polyèdre convexe, cela est plus surprenant pour une stellation de l'icosaèdre régulier ! Ces polyèdres à symétrie tétraédrale ont été décrits par George W. Hart (voir référence).
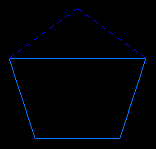
Pour le dodécaèdre on tronque complètement (par les trois sommets adjacents) quatre sommets appartenant à un tétraèdre inscrit ; 4 faces triangulaires apparaissent et les 12 pentagones sont transformés en trapèzes isocèles.
|
|
|
 |
Pour l'icosaèdre on limite la première stellation (augmentation par une pyramide triangulaire) à quatre faces appartenant à un tétraèdre circonscrit ; 4 faces triangulaires disparaissent et 12 autres sont transformées en cerfs-volants.
|
|
|
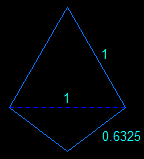 |
| Dans les deux cas on obtient un polyèdre convexe à 16 faces (4 triangles et 12 quadrilatères), 16 sommets et 30 arêtes qui a les mêmes sept axes de symétrie que le tétraèdre mais pas de plans de symétrie.
On est parti de deux polyèdres duals sur lesquels on a effectué des manipulations duales ; il n'est donc pas étonnant d'obtenir deux polyèdres topologiquement identiques qui ont la même forme canonique (un hexadécaèdre géométriquement autodual). |
|
|
| Si on tronque huit sommets d'un dodécaèdre appartenant à un cube, on obtient un icosaèdre d'or (8 faces sont des triangles équilatéraux, les 12 autres sont des triangles d'or) qui a une symétrie tétraédrique (seulement trois plans de symétrie). |
|
|
| Si on effectue la première stellation de l'icosaèdre sur quatre paires de faces opposées, 8 faces disparaissent et il reste un dodécaèdre équifacial (les faces sont des pentagones symétriques) ; il est donc topologiquement identique au dodécaèdre régulier, mais avec une symétrie tétraédrique (seulement trois plans de symétrie). | ||
| Le tétartoïde des minéralogistes est un autre dodécaèdre équifacial (les faces sont des pentagones irréguliers) topologiquement identique au dodécaèdre régulier avec une symétrie tétraédrique (pas de plans de symétrie). |
| |
| références : (en anglais) |
http://www.georgehart.com/virtual-polyhedra/tetrahedrally_stellated_icosahedron.html par George W. Hart
pyritohedral icosahedron et pyritohedron sur Polytope Wiki |
page accueil
 |
polyèdres convexes - polyèdres non convexes - polyèdres intéressants - sujets connexes | février 2004 mis à jour 03-22-2013 |