If it seems natural that a truncation of the regular dodecahedron leads to a convex polyhedron, it is more surprising for a stellation of the regular icosahedron! These polyhedra with tetrahedral symmetry have been described by George W. Hart (see reference).
For the dodecahedron we completely truncate (through the three adjacent vertices) four vertices which belong to an inscribed tetrahedron; 4 triangular faces appear and the 12 pentagons are transformed into isosceles trapeziums.
|
|
|
 |
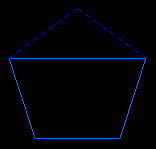
For the icosahedron we restrict the first stellation (augmentation by a triangular pyramid) to four faces which belong to a circumscribed tetrahedron; 4 triangular faces disappear and 12 others are transformed into kites.
|
|
|
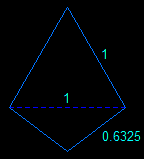 |
| In both cases we get a convex polyhedron with 16 faces (4 triangles and 12 quadrilaterals), 16 vertices and 30 edges which has the same seven symmetry axes as the tetrahedron but no planes of symmetry.
We started with two dual polyhedra on which dual manipulations have been performed; therefore it is no surprising to get two topologically identical polyhedra which have the same canonical form (a geometrically autodual hexadecahedron). |
|
|
| If we truncate eight vertices of a dodecahedron belonging to a cube we get a golden icosahedron (8 faces are equilateral triangles, the 12 others are golden triangles) which has tetrahedral symmetry (only three planes of symmetry). |
|
|
| If we perform the first stellation of the icosahedron on four pairs of opposite faces, 8 faces disappear and it remains an equifacial dodecahedron (the faces are symmetric pentagons); thus it is topologically identical to the regular dodecahedron, but with a tetrahedral symmetry (only three planes of symmetry). | ||
| The mineralogist's tetartoid is an other equifacial dodecahedron (the faces are irregular pentagons) topologically identical to the regular dodecahedron with a tetrahedral symmetry (no planes of symmetry). |
| |
| references : |
http://www.georgehart.com/virtual-polyhedra/tetrahedrally_stellated_icosahedron.html by George W. Hart
pyritohedral icosahedron and pyritohedron on Polytope Wiki |
home page
 |
convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects | February 2004 updated 03-12-2013 |