dessins des T-shirts "AMC - Nouméa"
Australian Mathematics Trust

dessins des T-shirts "AMC - Nouméa" |
 Australian Mathematics Trust |
 |
 |
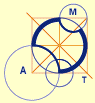
2009 Cette année nous réutilisons le dessin de 2000 :
Une occasion de revoir l'inversion, une passionnante transformation géométrique malheureusement un peu tombée dans l'oubli. Remarque : le grand cercle extérieur du dessin précédent a été remplacé par un carré ; dans les deux cas ils ne servent qu'à limiter la taille du dessin, les quatre régions extérieures, images des quatre carrés centraux, étant infinies. dessin de Maurice Starck | ||

dessin de Maurice Starck d'après une idée de Bruce Henry (Melbourne) Remarque : parmi les 35 hexaminos on trouve les 11 patrons du cube.
|
2008
Un puzzle pour écrire AMC dont les 1+1+2+5+12+35=56 pièces sont tous les polyminos (assemblages de carrés) d'ordres 1 à 6.
http://www.jlsigrist.com/polyminos.html Questions ouvertes : Combien y a-t-il de façons différentes (à symétrie ou rotation près) de réaliser ce dessin ? Combien y a-t-il de "bons coloriages" (conformes au théorème des quatre couleurs) différents ? | ||

dessin de Nicolas Hannachi et Maurice Starck réalisé avec Mathematica |
2007
Une infinité de cercles quatre à quatre mutuellement tangents
Les nombres indiqués sur les disques sont les courbures (inverses des rayons) ; la formule de Descartes (en dessous) donne la relation entre les courbures de quatre cercles tangents deux à deux. Cette configuration est remarquable car toutes les courbures sont entières.
voir la page "Kissing Circles" sur le site math à mâter de Nicolas Hannachi
| ||
dessin de Maurice Starck |
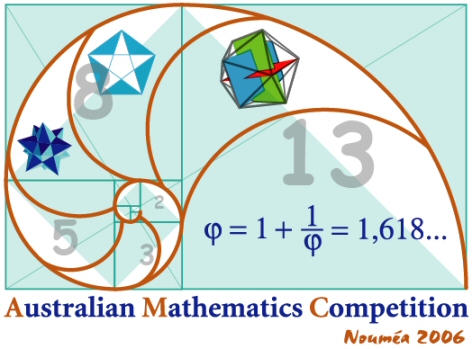
2006
Une adaptation du projet de timbre poste consacré au nombre d'or.
| ||
 |
2005
Ce joli puzzle est formé de dix pièces, les hexaminos (tous les assemblages possibles de trois ou quatre hexagones réguliers).


dessins de Bruce Henry (Melbourne) http://www.mathematische-basteleien.de/hexominos.htm | ||

pavage hyperbolique {10,3} illustré à la manière d'Escher. Cette image a été réalisée et mise à notre disposition par Doug Dunham. Il est tentant de conjecturer que les lignes blanches sont des "droites" (hyperboliques), mais ce n'est pas le cas ; il s'agit de "courbes équidistantes" aux "droites" passant par les mêmes points du cercle limite. |
2004
Retour aux pavages hyperboliques, avec un dessin "à la manière de M.C. Escher", plus coloré que celui utilisé en 1999.
Références :
| ||
 |
2003
La divine proportion, connue depuis l'Antiquité, a depuis été largement utilisée en peinture et en architecture. Le pentagone régulier retient tout naturellement l'attention (le rapport de sa diagonale à son côté est égal au nombre d'or).
dessin de Maurice Starck réalisé avec Cabri-Géomètre | ||

image "artistique" de l'ensemble de Mandelbrot
|
2002
L'ensemble de Julia Jc est formé par les nombres complexes dont la suite des itérés par le polynôme z²+c reste bornée. Les ensembles Jc varient beaucoup en fonction de c.
Pour en savoir plus sur ces ensembles remarquables quelques références parmi beaucoup d'autres :
| ||

dessin de Maurice Starck réalisé avec Cabri-Géomètre |
2001
Ce dessin est un diagramme de Venn d'ordre 5 avec un coloriage binaire.
La première animation montre des diagrammes de Venn symétriques, d'ordres 2 à 7 (4 à 128 régions).
Référence :
http://www.combinatorics.org/files/Surveys/ds5/VennEJC.html
| ||
 |
 | ||
 |
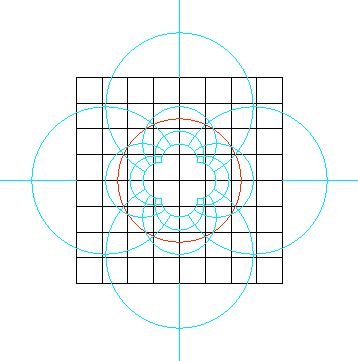
2000
Ce dessin illustre une transformation géométrique délaissée, l'inversion ; il s'agit d'une superposition d'un échiquier et de son inverse.
Outre le côté esthétique du dessin, le thème de l'échiquier est symbolique à bien des égards... dessins de Maurice Starck réalisés avec Cabri-Géomètre | ||
|
Une inversion est définie par PM'xPM=r² (P, M et M' alignés, M et M' du même côté du pôle P). L'ensemble de ses points fixes est le cercle de centre P et de rayon r (cercle d'inversion).
Ainsi un quadrillage (en noir) est transformé en un pavage (en bleu) formé de deux droites et d'arcs de cercles mutuellement orthogonaux.
|
 | ||

pavages hyperboliques : {6,4} en rouge, le dual {4,6} en bleu clair,
dessin de Maurice Starck réalisé avec Cabri-Géomètre |
1999
Cette rosace est une figure de géométrie hyperbolique. Le modèle est le disque de Poincaré où les "droites" sont les arcs orthogonaux au bord (la somme des angles d'un triangle y est inférieure à un plat). Le dessin montre des "pavages réguliers" en hexagones (rouge), en losanges (bleu clair) et en triangles rectangles (angles de 90, 45 et 30°).
| ||
 |
1998
Outre son indéniable caractère esthétique, ce dessin, constitué d'une suite de polygones réguliers emboîtés, illustre un vrai problème : quelle est la limite de la suite des rayons des cercles ? Solution trouvée sur internet (janvier 2004) : environ 8,7, ce qui correspond à la valeur "expérimentale" que l'on peut "mesurer" en remarquant que les sommets des polygones se trouvent sur des ellipses tangentes en un point commun que l'on peut "estimer" : valeur limite des rayons ≈ grand axe de la petite ellipse / rayon du petit cercle
dessin de Maurice Starck réalisé avec Cabri-Géomètre | ||