net by Peter R. Cromwell
Robert Connelly's "sphere" (1978)is the fir st example of a non-self-intersecting flexible polyhedron; a model simplified by Kuiper and Deligne has 18 faces and 11 vertices.
Two important results concerning the flexible polyhedra:
• A convex polyhedron is rigid. (rigidity conjecture proposed by Euler in 1766, proved for the convex polyhedra by Cauchy in 1813).
• During the deformation of a flexible polyhedron its volume remains constant. (bellow's conjecture, Connelly-Sabitov-Walz, 1997)
|
|
net by Peter R. Cromwell |
| The LiveGraphics3D applet has some difficulties to well display faces which are almost coplanar. | |
| This shaky polyhedron - infinitesimally flexible - may be constructed by replacing six pairs of equilateral triangles in a regular icosahedron with pairs of isosceles triangles; the bases of the isosceles triangles are the great sides of three rectangles two by two orthogonal and with sides' ratio 2.
It can be very lightly deformed by acting on the angles of the pairs of the isosceles triangles. All its dihedral angles are right (adjacent faces are orthogonal). The centers of the eight remaining equilateral faces are the vertices of a cube (use the F key to see it). Beware! the convex envelope is a non regular icosahedron sometimes called pseudo-icosahedron; it also has six pairs of isosceles faces and only three planes of symmetry. Remark: If this icosahedron is constructed with paper (non rigid faces) then the isosceles triangles may be folded inside by pairs to get a regular octahedron. |
|
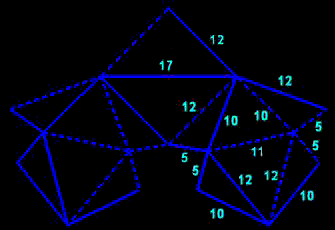
| This deltahedron is the assembly of two polyhedral surfaces: an icosahedron with a "hole" corresponding to two adjacent faces, and a pair of octahedra with a "hole" of the same type; it therefore has 20+2x8-6=30 faces, 12+9-4=17 vertices and 29+20-4=45 edges. If the two components are clearly flexible, this is not obvious for the final polyhedron; however, it suffices to pinch two opposite vertices common to the two components to be convinced of this.
But an observation is not a proof! Melinda suggests to ask an AI (ChatGPT or Le Chat) for a proof... |
| references: |
• Steffen's polyhedron on MathWorld and on mathematik.com
• Rigidity of Polyhedra web pages (McGill University - Montréal, illustrated by J.Shum) • The Bellows Conjecture by Ian Stewart • Les polyèdres flexibles et la conjecture du soufflet by Thierry Lambre (bulletin 471 APMEP, page 533, in French) • Polyhedra by Peter R. Cromwell (Cambridge University Press - 1997, pages 239-246) • The Penguin Dictionary of Curious and Interesting Geometry by David Wells (Penguin, London - 1991, page 161) • How "shaky" is the Jessen's orthogonal icosahedron? |
home page
 |
convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects | November 2003 updated 19-12-2023 |