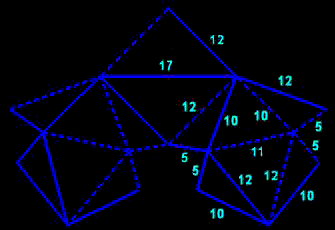
patron de Peter R. Cromwell
Les octaèdres de Bricard (1897) : assemblages de deux "pyramides carrées", ils ont des faces qui se coupent et ne peuvent donc être réalisés que comme structures articulées de douze "arêtes" (Raoul Bricard était un ingénieur français)
La "sphère" de Connelly (1978) est le premier exemple de polyèdre flexible non croisé ; un modèle simplifié par Kuiper et Deligne a 18 faces et 11 sommets.
Deux résultats importants concernant les polyèdres flexibles :
• Un polyèdre convexe est rigide. (conjecture de rigidité proposée par Euler en 1766, prouvée pour les polyèdres convexes par Cauchy en 1813).
• Lors de la déformation d'un polyèdre flexible son volume reste constant. (conjecture du soufflet, Connelly-Sabitov-Walz, 1997)
|
|
| |
| L'applet LiveGraphics3D a quelques difficultés pour bien afficher des faces qui sont presque coplanaires. | ||
| Ce polyèdre "branlant" - flexible de manière infinitésimale - peut être construit en remplaçant six paires de triangles équilatéraux d'un icosaèdre régulier par des paires de triangles isocèles ; les bases des triangles isocèles sont les grands côtés de trois rectangles deux à deux orthogonaux et dont le rapport des côtés est 2.
Il peut être très légèrement déformé en agissant sur les angles des paires de triangles isocèles. Tous ses angles dièdres sont droits (des faces adjacentes sont orthogonales). Les centres des huit faces équilatérales restantes sont les sommets d'un cube (utiliser la touche F pour le voir). Attention ! l'enveloppe convexe est un icosaèdre non régulier parfois appelé pseudo-icosaèdre ; il a aussi six autres paires de faces isocèles et seulement trois plans de symétrie. Remarque : Si on réalise cet icosaèdre en papier (faces non rigides) on peut replier les triangles isocèles par paires à l'intérieur pour obtenir un octaèdre régulier. |
|
| Ce deltaèdre est l'assemblage de deux surfaces polyédrales : un icosaèdre avec un "trou" correspondant à deux faces adjacentes, et une paire d'octaèdres avec un "trou" du même type ; il a donc (8-2)x2 + (20-2) = 30 faces, 30 sommets et 45 arêtes. Si les deux composants sont clairement flexibles, ce pas évident pour le polyèdre final ; il suffit cependant de pincer deux sommets opposés communs aux deux composants pour s'en convaincre.
Mais un constat n'est pas une preuve ! Melinda suggère de demander une preuve à ChatGPT ou à une IA concurrente. |
| références : |
• le polyèdre de Steffen sur MathWorld et sur mathematik.com (en anglais)
• Rigidity of Polyhedra pages web en anglais (Université McGill - Montréal, illustrées par J.Shum) • The Bellows Conjecture par Ian Stewart • Les polyèdres flexibles et la conjecture du soufflet de Thierry Lambre (bulletin 471 de l'APMEP, page 533) • Polyhedra de Peter R. Cromwell (Cambridge University Press - 1997, page 239-246, en anglais) • Dictionnaire Penguin des curiosités géométriques de David Wells (éditions Eyrolles - 1997, pages 150-151) • How "shaky" is the Jessen's orthogonal icosahedron? |
page accueil
 |
polyèdres convexes - polyèdres non convexes - polyèdres intéressants - sujets connexes | novembre 2003 mis à jour 19-12-2023 |