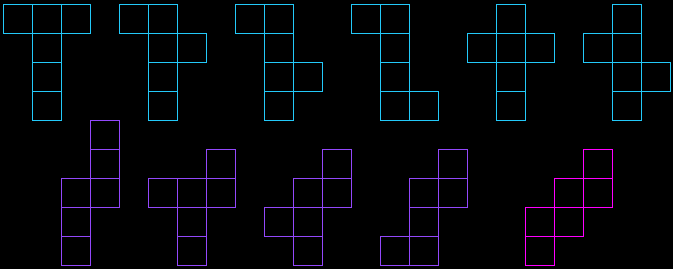
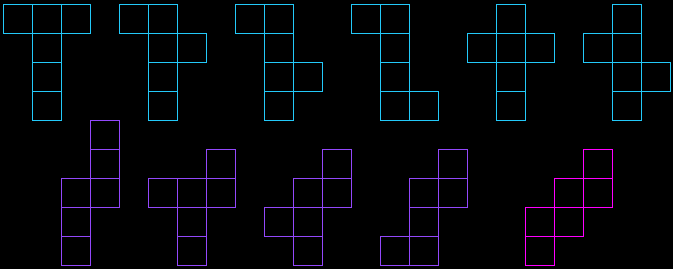
No more than four squares can be aligned (lateral surface of the prism). We get six nets by arranging one square (base) on each side. If we don't allow to line up more than three squares, we discover four new nets. At last, if we align only two squares (the minimum), we find a last net. There is obviously no other arrangement possible.
Exercise: By reasoning in a similar way, find the eleven nets of the regular octahedron (note that it is an antiprism).
home page
 |
convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects | November 1999 updated 08-11-2014 |