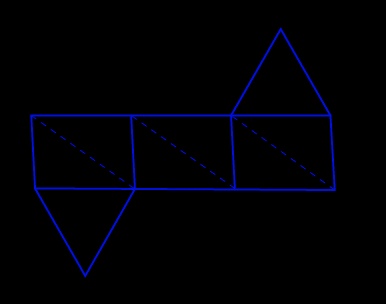
The three dashed diagonals show "valley folds". |
The three dashed diagonals show "valley folds". |
|
This net can lead to two distinct polyhedra which derive from a triangular prism by about 15° and 50° twists.
If you build a model out of thin card, you find that the two positions are interchangeable: a light pressure and the model jumps from one position to the other. To build your own model you may download and print the net (PDF file).
Problem: We "open" two regular bipyramids of same order n by duplicating a vertex of the common base; can we fit these two sets of 2n equilateral triangles together, one orthogonal to the other, in order to build a deltahedron with 4n faces?
The hight 2h of one of the two "open bipyramids" must be equal to the width 2d of the opening of the other (edges of length 1).
Answer by Michael Goldberg (1978): Yes for the three configurations!
order 3: d = h = 0.64459... (convex deltahedron D12) |
order 4: d = h = 0.42394... |
| Calculations show that, in the configuration of order 5, we get a tristable icosahedron (with two symmetric positions); if we lightly "crush" one of the "bipyramids" along its axe to diminish its high, the high of the other grows:
d1 = 0.071..., h1 = 0.49...
|
|
If, in the configuration of order 3, we replace the equilateral triangles with isosceles triangles (whose apex angle is slightly more than 103°), we get a tristable dodecahedron.
| references: |
• The Penguin dictionary of curious and interesting geometry by David Wells (Penguin Books - 1991)
• Polyhedra by Peter R. Cromwell (Cambridge University Press - 1997) pages 222-224 |
home page
 |
convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects | November 2003 updated 13-12-2003 |