some technical informations

regular polyhedra

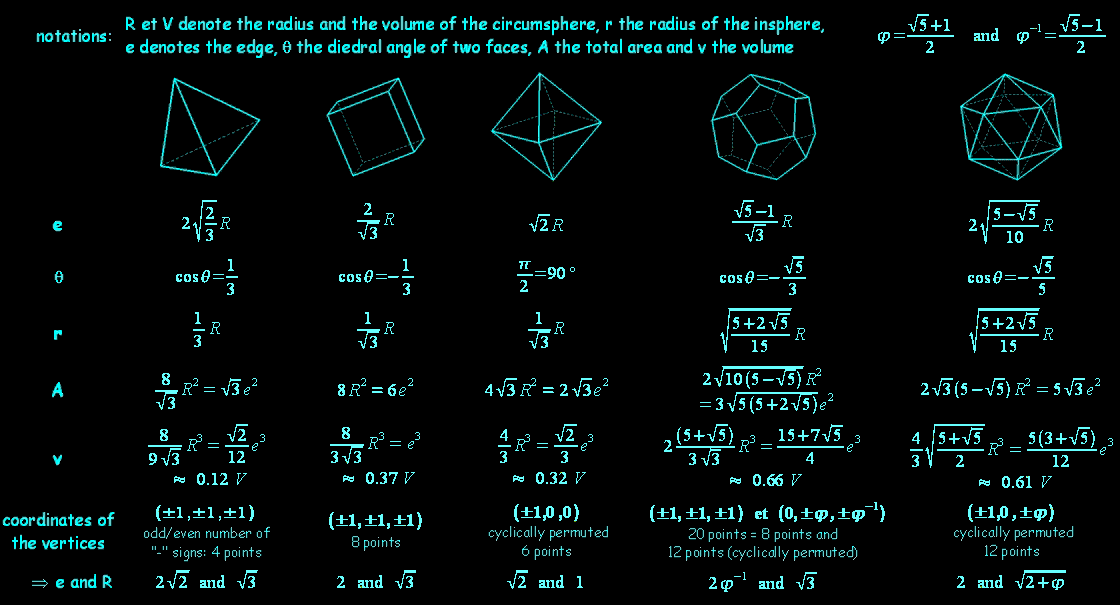
infos 1

groups of isometries

infos 2

semi-regular polyhedra

infos 3
infos 4 The snub cube and the snub dodecahedron may be obtained from the two regular polyhedra: first perform a similitude on each of its faces (center of the similitude on the center of the face), then truncations to create the chains of triangular faces around the transformed faces.
            cube : 16° 28'   and   0,4376     -     dodecahedron : 13° 6'  and   0,5621

Coordinates of the vertices of the rhombic semi regular polyhedra:

dodecahedron:   (±1, ±1, ±1)    8 points   and   (0, 0, ±3/2)   cyclically permuted   6 points
triacontahedron:   (±φ, ±φ, ±φ)    8 points   and  (0, ±1, ±(1+φ))   cyclically permuted   24 points

Among the vertices of the rhombic dodecahedron we recognize those of a cube and those of a regular octahedron.
Among the vertices of the rhombic triacontahedron we recognize those of a regular dodecahedron (thus also those of a cube) and those of a regular icosahedron.

Rotations in space belong to the necessary tools to describe polyhedra. Mathematica defines a rotation using Euler's angles, but it is more convenient to use the matrix of a rotation of angle α  around an axis defined with an unit vector {u,v,w}: matrix
reference: "Mémoire sur la théorie des polyèdres" by M.E.Catalan (Journal of the Imperial Polytechnic School  - folio XLI - 1865)
"Improve, on some important point, the geometric theory of the polyhedra." (in French)
(great mathematics prize of the Sciences Academy - Paris 1863)

home page
French 		convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects September 1999
updated 17-07-2007