deux cubes pliants-dépliants

Les métamorphes sont de curieux objets qui admettent un cycle complet de transformations quand on les manipule.
Les IsoAxis et les kaléïdocycles, dont toutes les charnières sont activées simultanément, sont des diamorphes ; les deux exemples ci-dessous font partie des orthomorphes qui se transforment en activant alternativement des charnières orthogonales.
Il existe aussi des métamorphes plans des deux types, les flexagones (leur manipulation se fait cependant en 3D).

Soyez patients pendant l'initialisation !

un cube de Yoshimoto

l'assemblage classique de huit cubes

avec huit "demi-cubes" l'octaèdre tronqué (bleu clair)
remplirait exactement la cavité dans le cube de départ
On peut évidemment réaliser un cube de Yoshimoto en assemblant convenablement huit cubes ;
les segments magenta indiquent les huit arêtes de liaisons (six sont deux à deux alignées dans le cube).

Un patron complet n'est pas facile à imaginer ; celui ci-dessous a été conçu par Robert Byrnes
(un fichier PDF contient ce patron au format A4).

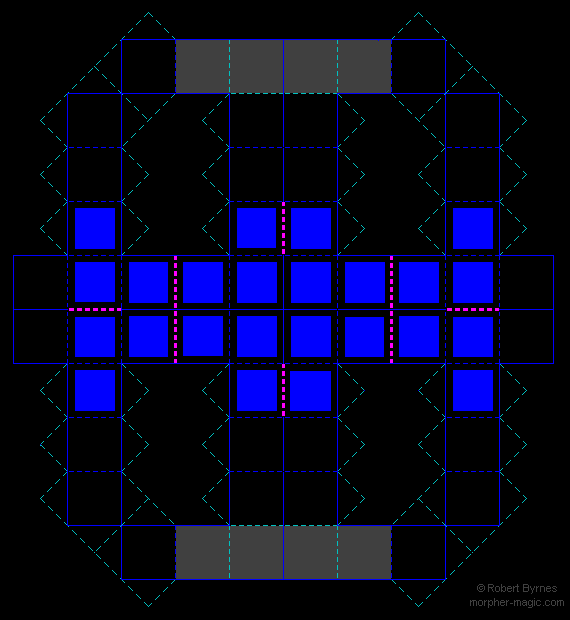cube de Yoshimoto Les pointillés magenta indiquent les huit arêtes de liaisons (attention à ne pas les couper !). Les pattes triangulaires sont destinées au collage.
Les carrés gris seront cachés à l'intérieur de quatre petits cubes ; replier les deux carrés de chaque paire l'un contre l'autre puis sous le carré adjacent (selon les deux pointillés bleu clair). Il y a donc deux types de patrons du cube (n° 1 et n° 4 de la liste).
Chaque petit cube a trois faces de chacune des deux couleurs ; pendant la manipulation le grand cube change de couleur (24 carrés d'une couleur sont visibles et les 24 autres sont cachés).

un cube de Byrnes

LiveGraphics3D a quelques difficultés à bien afficher toutes les faces

Réaliser ce curieux objet n'est pas très difficile : les arêtes sont proportionnelles à 6:3:2 et les segments magenta indiquent les huit arêtes de liaisons (deux à deux alignées dans le cube).

Robert Byrnes en présente un patron coloré dans son livret consacré aux métamorphes.


références : •  Metamorphs  par Robert Byrnes, en anglais (Tarquin - 2004), avec 14 patrons de kaléïdocycles, flexagones et orthomorphes
•  Mathematical Curiosities  par Gerald Jenkins et Magdalen Bear, en anglais (Tarquin Publications - 2000), avec patrons
•  The magic of flexagons  par David Mitchell, en anglais (Tarquin Publications - 1998), avec 10 patrons
•  objets convertibles (en anglais) : flyping-games  -   tangletoys

page accueil
anglais 		polyèdres convexes - polyèdres non convexes - polyèdres intéressants - sujets connexes août 2004
mis à jour 12-03-2007