the cube with edge a+b
(a+b)3 = a3 + 3a2b + 3ab2 + b3
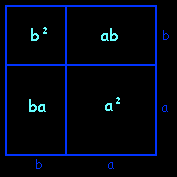
(a+b)2 = a2 + 2ab + b2
The idea of this cutting of the cube comes from a visitor, Pierre Lavastre.
the cube with edge a+b |
(a+b)3 = a3 + 3a2b + 3ab2 + b3 | |
(a+b)2 = a2 + 2ab + b2
|
||
| This identity is easy to visualize by cutting a square with side a in a corner of a square with side (a+b); the area of the big square is then equal to the sum of the areas of the four quadrilaterals (two squares and two identical rectangles). | Likewise we may visualize the cube of a sum by cutting a cube with edge a in a corner of a cube with edge (a+b); the volume of the big cube is then equal to the sum of the volumes of the eight cobblestones (two cubes and six rectangular parallelepipeds of two kinds). The idea of this cutting of the cube comes from a visitor, Pierre Lavastre. |
Question: can we "visualize"" (a+b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4 with the help of a 4D-hypercube?
the permutohedron |
|
| The 24 vertices of the truncated octahedron allow to represent the 4!=1x2x3x4=24 permutations of the symmetric group S4. Each vertex represents a permutation of a set {a,b,c,d} of four elements, with swaps along the edges (two elements are exchanged).On two opposite hexagons the vertices of one of them represent the six permutations which leave one element invariant, and we move to the vertices of the other by circular permutations. The permutations which are on the vertices of two opposite squares are represented with the same two pairs, in the same order on each square . | |
the associahedron |
|
| An associatope is a Stasheff polytope which allows to represent the Catalan number an=C(2n,n)/(n+1) in an (n-1)D space.
an=a0an-1 + a1an-2 + ... + an-1a0 with a0=1 and a1=1. They appear in many combinatorial problems: • the number of ways in which n-1 pairs of parentheses can be placed in a product of n+1 factors (at the vertices of a face the expressions have a common pair of parenthesis, ands along the edges one pair of parenthesis is moved), • the number of ways a (n+2)gone can be cut into n triangles with a common vertex, • the number of binary trees with n+1 leaves, • on an n-by-n grid the number of paths of length 2n joining the ends of a diagonal, remaining all on the same side. | |
two generalized associahedra (the cyclohedron and the H3) | |
|
|
|
| references: |
• Research/Mathematics of the Permutahedron and Associahedron with photos
• Catalan numbers by Robert M. Dickau • permutations and symmetric group (Wikipedia) |
home page
 |
convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects | January 2005 updated 31-07-2005 |