le cube d'arête a+b
(a+b)3 = a3 + 3a2b + 3ab2 + b3
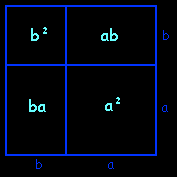
(a+b)2 = a2 + 2ab + b2
L'idée de ce découpage du cube vient d'un visiteur, Pierre Lavastre.
le cube d'arête a+b |
(a+b)3 = a3 + 3a2b + 3ab2 + b3 | |
(a+b)2 = a2 + 2ab + b2
|
||
| Cette identité est facile à visualiser en découpant un carré de côté a dans un coin d'un carré de côté (a+b) ; l'aire du grand carré est alors égale à la somme des aires des quatre quadrilatères (deux carrés et deux rectangles identiques). | De même on peut visualiser le cube d'une somme en découpant un cube d'arête a dans un coin d'un cube d'arête (a+b) ; le volume du grand cube est alors égal à la somme des volumes des huit pavés rectangles (deux cubes et six parallélépipèdes de deux types). L'idée de ce découpage du cube vient d'un visiteur, Pierre Lavastre. |
Question : peut-on "visualiser" (a+b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4 à l'aide d'un 4D-hypercube ?
le permutaèdre |
|
Les 24 sommets de l'octaèdre tronqué permettent de représenter les 4!=1x2x3x4=24 permutations du groupe symétrique S4. Chaque sommet représente une permutation d'un ensemble {a,b,c,d} à quatre éléments, et en suivant une arête on effectue une transposition (deux éléments sont échangés).Si on examine deux hexagones opposés, les sommets de l'un représentent les six permutations qui laissent un élément invariant, et on passe aux sommets de l'autre par permutations circulaires. Les permutations que l'on trouve aux sommets de deux carrés opposés sont représentées par les mêmes deux paires, dans le même ordre sur chaque carré. | |
l'associaèdre |
|
Un associatope est un polytope de Stasheff permettant de représenter le nombre de Catalan an=C(2n,n)/(n+1) dans un (n-1)D espace.
an=a0an-1 + a1an-2 + ... + an-1a0 avec a0=1 et a1=1. Ils apparaissent dans de nombreux problèmes de combinatoire : • le nombre de façons de placer n-1 paires de parenthèses dans un produit de n+1 facteurs (aux sommets d'une face les expressions ont une paire de parenthèses en commun, et aux extrémités d'une arête elles différent par une paire), • le nombre de façons de découper un (n+2)gone en n triangles avec un sommet commun, • le nombre d'arbres binaires à n+1 feuilles, • sur une grille n-par-n, le nombre de chemins de longueur 2n joignant les extrémités d'une diagonale, tous entièrement du même côté. | |
deux associaèdres généralisés (le cycloèdre et le H3) | |
|
|
|
| références : |
• Research/Mathematics of the Permutahedron and Associahedron (en anglais) avec photos
• Catalan numbers (en anglais) par Robert M. Dickau • permutations et groupe symétrique (Wikipedia) |
page accueil
 |
polyèdres convexes - polyèdres non convexes - polyèdres intéressants - sujets connexes | janvier 2005 mis à jour 31-07-2005 |