tP and eP are dual; the same holds for P1 and P1' and for P2 and P2'.
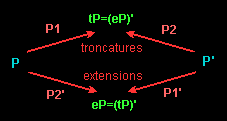
| The truncations (cuttings of regular pyramids on each vertex) of two regular dual polyhedra P and P' give the same polyhedron tP. Their extensions (assemblings of regular pyramids on each face) give the same polyhedron eP.
tP and eP are dual; the same holds for P1 and P1' and for P2 and P2'. |
 |
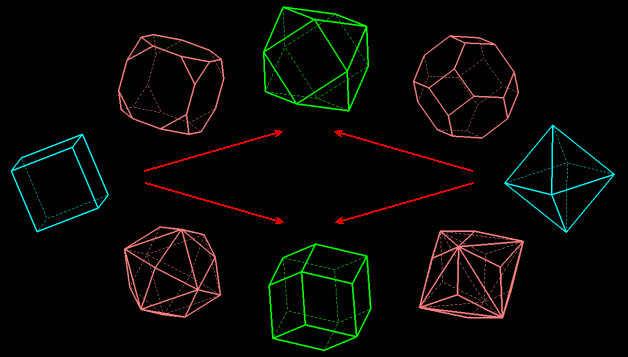
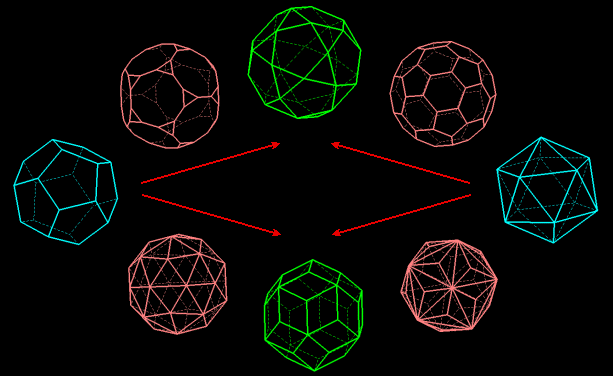
The snub cube and the snub dodecahedron - which can't be obtained by truncations - and their duals are absent.
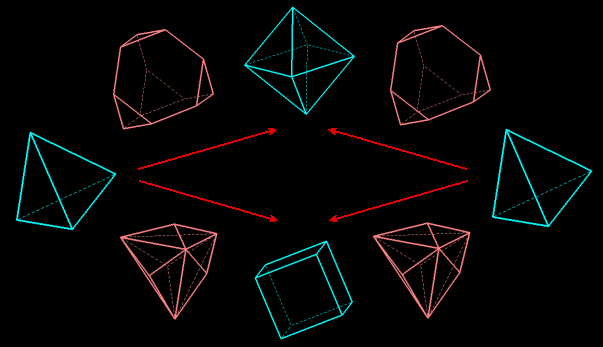
The tetrahedron is its own dual, thus its sequences are very poor (and the snub tetrahedron is the regular icosahedron).
home page
 |
convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects | August 2002 updated 13-06-2020 |