 |
 |
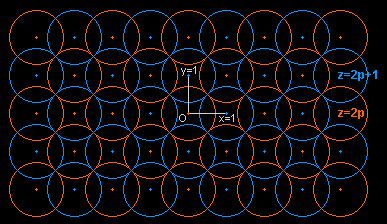
Un empilement compact de sphères identiques est un arrangement de densité (partie du volume occupé par les sphères) maximale. L'empilement périodique compact présenté ci-dessus à gauche (les couches orange ont une altitude paire 2p, et les bleues une altitude impaire 2p+1) est l'empilement cubique compact ou CCP ("cubic close packing") ; sa densité est environ 0,74.
Le rayon des sphères est r=sqrt(2)/2 ("sqrt" signifie "racine carrée", de l'anglais "square root") ; les centres sont situés sur une grille
carrée diagonale et les sommes de leurs coordonnées sont toutes paires (elles sont impaires pour les centres des trous). Remarquons que chaque
sphère est entourée par douze sphères (4 de la même couleur et 2x4=8 de l'autre couleur) dont les centres sont les sommets d'un cuboctaèdre , et que si l'on écrase symétriquement cet empilement chaque sphère est déformée en un dodécaèdre rhombique (dual du cuboctaèdre).
Le CCP peut aussi être réalisé avec des couches où chaque sphère est entourée par six sphères (en haut à droite et ci-dessous au milieu) et touche trois sphères de la couche en dessous (bleue) et trois de plus de la couche au-dessus (verte).
Finalement il existe une troisième façon de regarder un CCP, encore une fois avec deux couches (ci-dessous à droite); mais cette fois les centres des sphères sont situés sur une grille rectangulaire. Neuf sphères constituent un prisme carré (huit aux sommets et une au centre) avec les rectangles comme faces latérales.
Steve Waterman a été le premier à mettre cette troisième propriété d'empilement en évidence.
|
|
|
|
Soyez patients pendant l'initialisation !
D'autres vues permettent de voir les blocs polyédriques et les différents polyèdres correspondants.
|
|
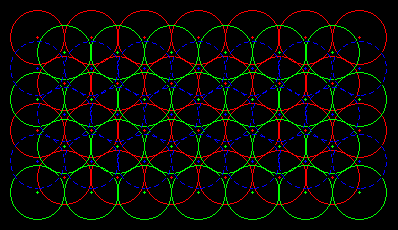
Le CCP peut être regardé avec trois couches (à gauche) ; il existe aussi une disposition différentes avec seulement deux couches qui constitue un autre empilement : l'empilement hexagonal compact ou HCP (à droite).
Dans un HCP les centres des douze sphères sont les sommets d'un polyèdre parfois appelé "anti cuboctaèdre", et, si cet empilement est écrasé, chaque sphère est déformée en un "anti dodécaèdre rhombique". |
|
| Pourquoi ces empilements sont-ils appelés "cubique" et "hexagonal" ?
Dans le CCP ou FCC ("face centered cubic") deux tétraèdres, chacun avec six sphères comme base et une comme sommet, constituent un cube (14 sphères en tout : 8 aux sommets et 6 aux centres des faces). Dans un HCP on peut mettre en évidence un prisme hexagonal. |
| Remarque :La disposition des sphères dans un CCP révèle une amusante propriété : les milieux des côtés de la base d'un tétraèdre trirectangle définissent un tétraèdre régulier de même hauteur.
Dans un cube unité le calcul des volumes des pyramides (respectivement 1/6 et 1/3) prouve le même résultat et de plus montre que les hauteurs valent un tiers et deux tiers de la diagonale du cube. |
|
|
| Sur la grille formée par les centres des sphères de diamètre sqrt(2) de l'empilement il y a trois polyèdres simples qui pavent l'espace :
• un cube centré en un vide, avec une arête de longueur 2, • un prisme hexagonal centré en un vide, avec une base de côté sqrt(2) et de hauteur 2sqrt(3)=h, • un prisme carré centré en un point, avec une base de côté sqrt(2) et de hauteur 2. remarques :
Les centres des trois types de polyèdres définissent trois nouvelles grilles (ci-dessous).
|
| |
|
|
|
|
Et pour ceux qui sont intéressés, d'autres fenêtres "pop-up" : trois assortiments des polyèdres, trois blocs des polyèdres, un bloc des cubes, un bloc des prismes hexagonaux, un bloc des prismes carrés, les trois grilles et les prismes associés à un cube (12 prismes carrés associés par paires aux faces du cube et 4 prismes hexagonaux d'axes les diagonales du cube).
On peut disposer les fenêtres pop-up en cascade au fur et à mesure de leur ouverture et les voir toutes en minimisant la fenêtre principale.
Les deux autres polyèdres classiques qui pavent l'espace, le dodécaèdre rhombique et l'octaèdre tronqué, apparaissent eux aussi dans le CCP.
Une dernière fenêtre pop-up avec un festival de tous ces polyèdres : une paire de cubes, un trio de prismes hexagonaux, une paire de prismes carrés, un dodécaèdre rhombique et un octaèdre tronqué.
Ne manquez pas les polyèdres de Waterman : une autre manière de définir des polyèdres avec le CCP.
Merci à Steve pour son aimable aide et ses suggestions pertinentes pendant l'élaboration de cette page.
| références : |
• les polyèdres de coordination en cristallographie (Bulletin de l'Union des Physiciens)
• cristallographie : introduction - cristallochimie - les systèmes cristallins - l'organisation des atomes - propriétés des minéraux |
page accueil
 |
polyèdres convexes - polyèdres non convexes - polyèdres intéressants - sujets connexes | décembre 2004 mis à jour 25-06-2005 |