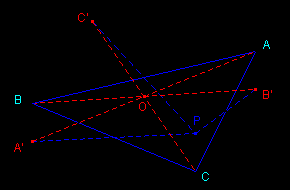
ABC is a triangle and P a point distinct from A, B and C. If A', B' and C' are the symmetric points of P with respect to the midpoints of the line segments (BC), (CA) and (AB) respectively, then the segments (AA'), (BB') and (CC') have same midpoint.
 |
 |
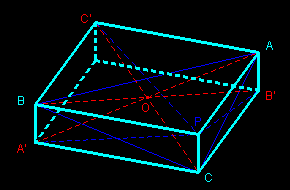
Since the segments (BA'), (PC) and (AB') are parallel and of same length (as opposite sides of parallelograms BA'CP and PCB'A) we can draw a parallelepiped in which the diagonal segments (AA'), (BB') and (CC') have same midpoint.
Let's note that the diagrams don't prove the property. We have completed the left one to get a riding prospect (parallel perspective) of a parallelepiped; it's the interpretation of the enriched diagram on the right which constitutes the proof.
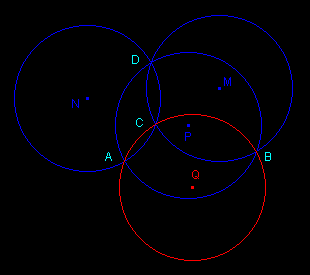
If three circles with same radius r concur, then their three other common points lay on a circle with radius r.
 |
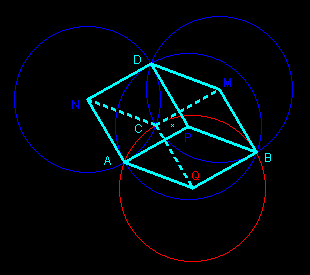 |
The three centers M, N and P and the four common points A, B, C and D are seven vertices of a cube represented in perspective with ratio 1. The last vertex Q is center of the circumcircle of ABC; its radius is also r.
proof: MCND, MBPD and NDPA are rhombuses with same side r : so are the quadrilaterals which represent the three other faces of the cube (central symmetry of the cube). The twelve edges are segments of same length r.
(ABCD) and (MNPQ) are symmetric (with respect to the center of the cube) orthocentric systems: each of the four points is orthocentre of the triangle defined by the three others.
proof: for example (AB) and (DC) are perpendicular: the diagonals of the rhombus MCND are perpendicular and the opposite sides of the parallelogram MNAB are parallel.
Two triangles are perspective from a point if their corresponding vertices are joined by concurrent lines. The point of concurrence is the perspective center.
Two triangles are perspective from a line if the extensions of the corresponding sides meet in collinear points. The line joining these points is the perspective axis.
Desargues' theorem guarantees that if two triangles are perspective from a point, they are perspective from a line (and if they are perspective from a line, they are perspective from a point).
If we consider the Desargues' configuration as a figure in the space (a tetrahedron cut by a plane), the proof of the theorem becomes obvious.
|
The two figures may be modified dynamically: all the big points can be moved with the mouse pointer. Desargues' theorem is a projective theorem: it remains true when the configuration is viewed in perspective.
| |
| references: |
• Symmetries in a triangle by Alexander Bogomolny
• The Penguin dictionary of curious and interesting geometry from David Wells (Penguin Books - 1991) • Johnson's theorem in 4D by Thérèse Eveilleau (in French) |
home page
 |
convex polyhedra - non convex polyhedra - interesting polyhedra - related subjects | September 1999 updated 17-11-2017 |