les trophées AMC - Nouvelle-Calédonie
Australian Mathematics Trust

les trophées AMC - Nouvelle-Calédonie |
 Australian Mathematics Trust |
 |

Cet objet est un assemblage de huit cubes en un grand cube que l'on peut manipuler de façon à faire apparaître successivement 24 ou 28 faces décorées de polyèdres (semi)réguliers. En configuration "cube" chaque face montre quatre carrés élémentaires ; en configuration "parallélépipède", les faces montrent huit, quatre et deux carrés. Le cycle complet se fait en 2+1+1+2+1+1 rotations par rapport à des axes orthogonaux.
Technique d'assemblage (═ et ll indiquent les charnières) et disposition des illustrations24 faces extérieures (deux à deux opposées en configuration "cube")
| 1 2 5 6 | 9 ═ 10 13 ═ 14 | 17 18 21 22 |
| ll ll | ll ll ll ll | |
| 3 4 7 8 | 11 12 15 16 | 19 20 23 24 |
illustrations en six planches de huit carrés (configurations "parallélépipède")
| 6 4 3 5 | 16 14 ═ 13 15 | 17 ═ 19 20 ═ 18 |
| ll ll | ||
| 8 2 1 7 | 11 9 ═ 10 12 | 22 ═ 24 23 ═ 21 |
| 25 26 ═ 27 28 | 33 34 35 36 | 41 ═ 42 43 ═ 44 |
| ll ll | ||
| 29 30 ═ 31 32 | 37 38 39 40 | 45 ═ 46 47 ═ 48 |
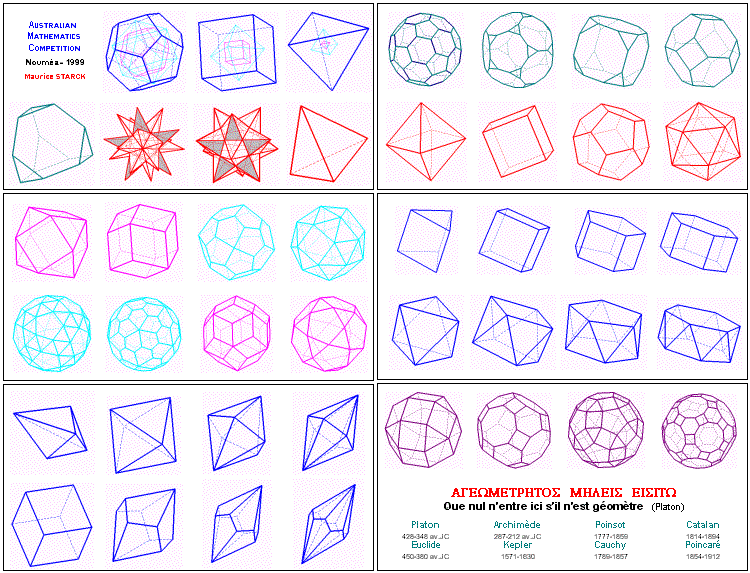
Table des illustrations
| 1 et 2 | petit et grand dodécaèdres étoilés | 21 à 24 | icosidodécaèdre, snub dodécaèdre et leurs duals | |
| 3 et 4 | cube et dodécaèdre régulier (avec leurs duals) | 25 à 28 | prismes réguliers (ordre 3 à 6) | |
| 5 | AUSTRALIAN MATHEMATICS COMPETITION | 29 à 32 | antiprismes réguliers (ordre 3 à 6) | |
| 6 | tétraèdre régulier (avec son dual) | 33 à 36 | diamants réguliers (ordre 3 à 6) | |
| 7 et 8 | tétraèdres (régulier et tronqué) | 37 à 40 | antidiamants réguliers (ordre 3 à 6) | |
| 9 à 12 | cube, dodécaèdre, octaèdre, icosaèdre (réguliers) | 41 et 42 | petit et grand rhombicuboctaèdres | |
| 13 à 16 | cube, dodécaèdre, octaèdre, icosaèdre (tronqués) | 43 et 44 | petit et grand rhombicosidodécaèdres | |
| 17 à 20 | cuboctaèdre, snub cube, et leurs duals | 45 à 48 | des mathématiciens qui ont étudié les polyèdres |
Les "polycubes" se sont avérés fragiles à l'usage, et leur réalisation artisanale - découpage des cubes et assemblage à l'aide de film transparent autocollant décoré de polyèdres - assez compliquée. Les polyèdres qui les remplacent sont robustes... mais ne peuvent être personnalisés. Un petit certificat attestera de leur origine.
Depuis 2005 cet assortiment de polyèdres est présenté dans une boîte gravée (avec le nom du lauréat, l'année et le niveau) réalisée en bois local (kaori).
 |
 |